Interacción de fuerzas Composición de Fuerzas Leyes de Newton Fuerzas y movimientos Movimiento planetario El universo actual Ley de gravedad universal Satélites terrestres Peso de los cuerpos La presión La presión hidrostática Principio de Arquímedes Presion atmosférica

El movimiento de los planetas

Los planetas, como todos los demás cuerpos celestes, no ocupan siempre la misma posición. ¿A qué ley física obedecen sus movimientos?

¿Está la Tierra en el centro del Universo?

Si observamos durante un día el recorrido del Sol, ¿diríamos que este gira alrededor de la Tierra o que la Tierra gira alrededor del Sol? Ciertamente, el sentido común indicar que es el Sol el que se mueve y que la Tierra permanece en reposo. Esto mismo se ha pensado durante una gran parte de la historia. Desde la Antigüedad se sabía que la Tierra era redonda (Eratóstenes, siglo III a.C.), pero, aunque Aristarco de Samos (en el siglo III a.C.) propuso un modelo heliocéntrico, las observaciones parecían favorecer un Universo geocéntrico. Así, en el siglo I, el griego Ptolomeo ideó un modelo geocéntrico basado en órbitas circulares, pues pensaba que la trayectoria circular era la más perfecta. Para explicar las observaciones, Ptolomeo introdujo órbitas excéntricas, lo que restaba sencillez.

El modelo heliocéntrico de Aristarco cayó en el olvido. Era demasiado adelantado para su época. Además, Aristarco incluso midió distancias y tamaños relativos del Sol y la Luna, y llegó a formular la hipótesis de que debía ser la Tierra el astro que girase alrededor del Sol, pues el diámetro del Sol era mayor y él pensaba que el astro menor (la Tierra) debía girar alrededor del mayor (el Sol), y no al revés.
En el siglo XVI, Nicolás Copérnico retomó el modelo heliocéntrico. Parece que conocía las ideas de Aristarco, pese a que los escritos no se habían conservado. En 1543, justo antes de su muerte, se publicó su obra cumbre, Revoluciones sobre los cuerpos celestes en la que proponía un modelo heliocéntrico, con el Sol en el centro del Universo y los planetas girando a su alrededor.

A Copémico le parecía muy complicado el modelo de Ptolomeo (el rey Alfonso X el Sabio dijo en el siglo XIII, a propósito del modelo de Ptolomeo, que si Dios le hubiese pedido su opinión al crear el Universo, le hubiese recomendado uno mucho más simple). Por ello ideó un modelo más sencillo para explicar las posiciones de los planetas. La aceptación de este modelo supuso décadas más tarde el despegue definitivo de las creencias científicas de los griegos: había comenzado la revolución científica.

Las leyes de Kepler


Las leyes de Kepler surgen para explicar matemáticamente el movimiento de los planetas alrededor del Sol. Se pueden considerar las precursoras de la Ley de la gravitación universal de Newton. En este apartado vamos a estudiar:

Primera ley de Kepler: ley de las órbitas
La primera ley, conocida como ley de las órbitas, acaba con la idea, mantenida también por Copernico, de que las órbitas debían ser circulares.
Los planetas giran alrededor del Sol siguiendo una trayectoria elíptica. El Sol se sitúa en uno de los focos de la elipse.
La excentricidad e de una elipse es una medida de lo alejado que se encuentran los focos del centro. Su valor viene dado por: 

 
Pues bien, la mayoría de las órbitas planetarias tienen un valor muy pequeño de excentricidad, es decir e ≈ 0. Esto significa que, a nivel práctico, pueden considerarse círculos descentrados.

Segunda ley de Kepler: Ley de las áreas
La segunda ley, conocida como ley de las áreas, nos da información sobre la velocidad a la que se desplaza el planeta. La recta que une el planeta con el Sol barre áreas iguales en tiempos iguales y para que esto se cumpla, la velocidad del planeta debe aumentar a medida que se acerque al Sol. Esto sugiere la presencia de una fuerza que permite al Sol atraer los planetas, tal y como descubrió Newton años más tarde.

Velocidad areolar Se define la velocidad areolar vA como el área barrida por el vector de posición de un cuerpo por unidad de tiempo. Según la segunda ley de Kepler, vA es constante. Por tanto:

En un instante, es decir, un diferencial de tiempo dt, el planeta se desplaza .Ya que se trata de un diferencial podemos considerar que    es una línea recta. Pues bien, los vectores  y ;determinan un paralelogramo cuya área es justo el doble que dA.
La segunda ley de Kepler establece que la velocidad areolar vA permanece constante a lo largo del recorrido del planeta. Por ello, dados dos puntos de la trayectoria cualesquiera, nos queda: 

Donde
  • r1 y r2 : Módulos de los vectores de posición del planeta en los puntos 1 y 2 respectivamente. Su unidad de medida en el Sistema Internacional es el metro (m)
  • v1 y v2 : Módulos de los vectores velocidad del planeta en los puntos 1 y 2 respectivamente. Su unidad de medida en el Sistema Internacional es el metro por segundo ( m/s)
  • θ1 y θ2 : Ángulos que forman los vectores de posición de los planetas con los de velocidad en los puntos 1 y 2 respectivamente. Su unidad de medida en el Sistema Internacional es el radián ( rad )

Perihelio: Es el punto de la órbita del planeta más próximo al Sol. La velocidad en las proximidades del perihelio es la máxima.
Afelio: Es el punto de la órbita del planeta más lejano al Sol. La velocidad en las proximidades del afelio es la mínima.

En el perihelio (p) y en el afelio (a) θ = 90º y por tanto:

Tercera ley de Kepler: Ley de los periodos

La tercera ley, también conocida como armónica o de los periodos, relaciona los periodos de los planetas, es decir, lo que tardan en completar una vuelta alrededor del Sol, con sus radios medios. Para un planeta dado, el cuadrado de su periodo orbital es proporcional al cubo de su distancia media al Sol. Esto es:


Donde:

  • T : Periodo del planeta. Su unidad de medida en el Sistema Internacional es el segundo (s)
  • k : Constante de proporcionalidad. Su unidad de medida en el Sistema Internacional es el segundo al cuadrado partido metro cúbico ( s2/m3 )
  • r : Distancia media al Sol. Por las propiedades de la elipse se cumple que su valor coincide con el del semieje mayor de la elipse, a. Su unidad de medida en el Sistema Internacional es el metro ( m )

Como consecuencia de esta ley, los planetas se mueven tanto más despacio cuanto mayor es su órbita. El valor concreto de la constante k será estudiado cuando hayamos introducido la ley de la gravedad formalmente. De momento si que señalaremos que su valor es el mismo para todos aquellos cuerpos que giran en torno a uno determinado. Así, por ejemplo, los planetas del Sistema Solar comparten el valor de k al girar todos ellos alrededor del Sol. También los satélites de un planeta compartirán un valor de k entre ellos. Es por ello que, en ocasiones, esta ley se presenta de acuerdo a la siguiente expresión:

 

Donde los subíndices 1 y 2 indican los periodos (T) , distancias medias ( r ) y longitud del semieje mayor (a = r ) de las órbitas de dos cuerpos que giran en torno a uno común, por ejemplo, dos planetas cualesquiera alrededor del Sol.

¿Cuándo se pueden usar las leyes de Kepler?

Kepler dedujo estas tres leyes a partir de la observación del movimiento de los planetas alrededor del Sol, y por ello, a lo largo de este apartado hemos enunciado las leyes en relación al Sol y a los planetas. Sin embargo, gracias a ellas podemos estudiar también:

El movimiento de cualquier cuerpo que orbite alrededor del Sol:

  • planetas
  • asteroides
  • cometas

Satélites orbitando alrededor de planetas

  • Naturales ( por ejemplo, la Luna )
  • Artificiales

La revolución galileana

A comienzos del siglo XVII, Galileo Galilei utilizó un sencillo telescopio y observó cuatro pequeños astros girando alrededor del planeta Júpiter: era la primera prueba de que astros que no giraban alrededor de la Tierra. Además, observó fases en Venus, confirmando el modelo heliocéntrico. había

La síntesis newtoniana

Ya a finales del siglo XVII, Isaac Newton estableció su famosa ley de la gravitación unive que explica los movimientos de los planetas (debido a fuerzas atractivas gravitatorias) y justificó de modo teórico las leyes de Kepler. Se dice que Newton, al observar la caída de una manzana del árbol por su propio peso, pensó que la misma fuerza que obligaba a caer a la manzana era responsable del movimiento de la Luna alrededor de la Tierra y por extensión, del movimiento de los planetas. Todo quedó entonces perfectamente cerrado. Además, con su ley de gravitación univers Newton predijo la trayectoria de los cometas (como el Halley).


Modelo geocéntrico Modelo geocéntrico
Este modelo fue una antigua teoría que sostiene que la tierra es el centro del universo, en este modelo se coloca la Tierra en el centro del Universo y los astros, incluido el Sol, girando alrededor de ella (geo: Tierra; centrismo: centro). Fue formulada por Aristóteles y estuvo en vigor hasta el siglo XVI, en su versión completada por Claudio Ptolomeo en el siglo II a. C.



Modelo heliocéntrico Modelo heliocéntrico
El modelo heliocéntrico es un modelo astronómico según el cual la Tierra y los planetas se mueven alrededor del Sol relativamente estacionario y que está en el centro del universo. Históricamente, el heliocentrismo se oponía al geocentrismo, que colocaba en el centro a la Tierra. La idea de que la Tierra gira alrededor del Sol fue propuesta desde el s. iii a. C. por Aristarco de Samos, pero no recibió apoyo de otros astrónomos de la antigüedad, no fue sino hasta el siglo XVI, durante el Renacimiento, cuando un modelo matemático completamente predictivo de un sistema heliocéntrico fue presentado por el matemático, astrónomo y clérigo católico polaco Nicolás Copérnico,​ con la publicación póstuma en 1543 del libro De Revolutionibus Orbium Coelestium. Esto marcó el inicio de lo que se conoce en Historia de la ciencia como «revolución copernicana». En el siguiente siglo, Johannes Kepler extendió este modelo para incluir órbitas elípticas. Su trabajo se apoyó en observaciones hechas con un telescopio que fueron presentadas por Galileo Galilei.



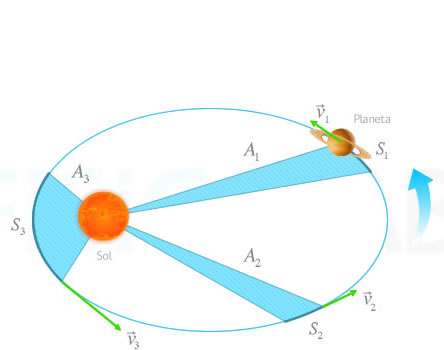Segunda Ley de Kepler Segunda Ley de Kepler
Suponiendo que el tiempo que se tarda en recorrer un espacio S1, S2 y S3 es el mismo, las áreas A1, A2 y A3 también serán iguales. Esto se debe a que a medida que disminuye la distancia al Sol, la velocidad aumenta (v1 < v2 < v3)



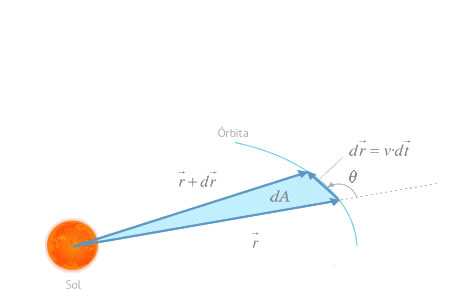En la siguiente imagen puedes observar el área correspondiente a dA, que supone la mitad de la del hipotético paralelogramo. En la siguiente imagen puedes observar el área correspondiente a dA, que supone la mitad de la del hipotético paralelogramo.