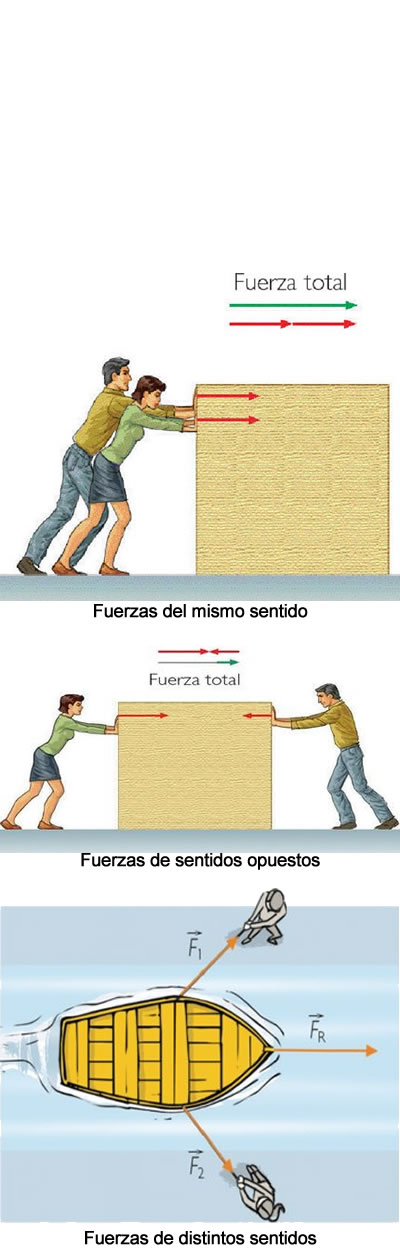
Composición de fuerzas
A menudo ocurre que dos o más fuerzas actúan sobre un cuerpo. En este caso, los efectos de cada una de ellas se suman o se restan, dando lugar a una fuerza resultante.
¿Cómo se representan las fuerzas?
La fuerza es una magnitud vectorial, al igual que la velocidad o la aceleración. Se representa por un vector F, que se caracteriza por cuatro datos:
- El módulo o intensidad es una medida cuantitativa de la fuerza. Si la intensidad es un número grande, la fuerza es grande; si, por el contrario, es un número pequeño, la fuerza es pequeña. La unidad en la que se mide la intensidad de una fuerza en el Sl es el newton (N).
- La dirección es la recta sobre la que se aplica la fuerza.
- El sentido indica hacia dónde se aplica la fuerza. En una misma dirección existen dos sentidos posibles.
- El punto de aplicación es el punto del espacio en que se aplica la fuerza. Esto es importante, pues los efectos que producen las fuerzas dependen en muchos casos del punto de aplicación
Composición de fuerzas
- Si las fuerzas tienen sentidos opuestos, sus efectos se restan. La fuerza resultante tendrá en este caso la misma dirección, estará orientada en el sentido de la fuerza de mayor módulo, y su módulo será igual a la resta de los módulos de ambas fuerzas.
- Si las fuerzas tienen el mismo sentido, sus efectos se suman. La fuerza resultante tendrá en este caso la misma dirección y sentido, y su módulo será igual a la suma de los módulos de ambas fuerzas.
- Si las fuerzas son perpendiculares, el cuadrado de la intensidad de la resultante será igual a la suma de los cuadrados de las intensidades de las fuerzas de partida (teorema de Pitágoras).
- Si las fuerzas forman un ángulo distinto de 90°, la suma o fuerza resultante, FR, coincide con la diagonal del paralelogramo construido sobre las fuerzas componentes o sumandos (regla del paralelogramo).
Descomposición de fuerzas
Hay ocasiones en las que resulta útil descomponer una fuerza FR en un sistema de dos o más fuerzas componentes, de forma que el efecto de FR sea igual al del conjunto del sistema.
La fuerza FR se ha descompuesto en sus dos componentes cartesianas, Fx y Fy
Fuerzas en equilibrio
En el caso de fuerzas con igual dirección y sentidos contrarios, ¿qué sucede si los valores de F₁y F₂ son iguales?
FR = F₁- F₂ = 0
Cuando sumamos dos fuerzas con la misma dirección, distintos sentidos y módulos iguales, la resultante es nula: FR = 0.
Solemos pensar que los cuerpos en reposo no están sometidos a fuerzas. Lo cierto es qu en general, los cuerpos en reposo interaccionan con otros cuerpos, normalmente también en reposo, de tal forma que las fuerzas sobre cada uno de ellos ejercidas por los otros se compensan.
Cuando la fuerza resultante es nula (no existen fuerzas o las fuerzas se compensan entre sí), el cuerpo está en equilibrio.
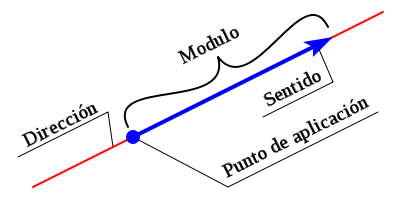 Fuerza es representada como un vector
Fuerza es representada como un vectorEl vector en el campo de la física, se define como un segmento de recta de longitud en forma de flecha, que consta de cuatro componentes y/o partes principales: el punto de partida, la magnitud, el sentido y la dirección. En este artículo, se hará alusión a la importancia del vector y la descripción general de las partes que le componen y que hacen que cumpla su propósito en términos de representación de magnitudes físicas vectoriales.