Difracción de la luz
Este fenómeno se genera cuando las ondas de luz atraviesan una rendija u orificio estrecho o cuando la curvatura de la luz pasa alrededor del borde de un objeto. La cantidad de flexión que posee dependerá del tamaño de la abertura en relación con la longitud de onda de la luz.
La difracción es un fenómeno característico del movimiento ondulatorio que se presenta cuando una onda es distorsionada por un obstáculo. Éste puede ser una pantalla con una pequeña abertura, una ranura que sólo permite el paso de una pequeña fracción de la onda incidente o un objeto pequeño, como un cable o un disco, que bloquea el paso de una pequeña parte del frente de onda. Por ejemplo, sabemos por nuestra experiencia diaria, en especial para el caso de las ondas sonoras y las ondas en la superficie del agua, que las ondas se extienden alrededor de los obstáculos que se interponen en su camino. Este efecto se hace cada vez más notorio a medida que las dimensiones de las ranuras o de los obstáculos se aproximan a la longitud de onda de las ondas.
Consideraremos sólo la difracción de Fraunhofer, que se presenta cuando las ondas incidentes son planas de manera que los rayos son paralelos- y observaremos el patrón a una distancia lo bastante grande para que sólo se reciban los rayos difractados paralelamente. Este fenómeno se conoce así por Joseph von Fraunhofer (1787-1826), quien fue uno de los primeros en estudiar el fenómeno.
Principio de Huygens
En 1680 aproximadamente, Christiaan Huygens (1629-1695) propuso un procedimiento geométrico para trazar la propagación de ondas elásticas o mecánicas en un medio material.
Una superficie de onda o frente de onda es una superficie compuesta por todos los puntos del medio que son alcanzados por el movimiento ondulatorio al mismo tiempo. Por consiguiente, todos los puntos de una superficie de onda se desplazan en fase.
Por ejemplo, para una onda plana que se propaga en la dirección del vector unitario u, la perturbación se expresa mediante f (ur-vt) y una superficie de onda está compuesta por todos los puntos en los que la fase u. r-ut tiene un mismo valor en un tiempo dado, así, la superficie de onda está dada por la ecuación u.r-vt = const que, para un tiempo t dado, corresponde a un plano perpendicular al vector unitario u. De manera parecida, para ondas esféricas, las superficies de onda están dadas por r - vt = const, donde r es la distancia a la fuente. Para un t dado, la superficie corresponde a una esfera con centro en la fuente.
Según Huygens, cuando el movimiento ondulatorio llega a la superficie de onda S, cada partícula a, b, c,... de la superficie se convierte en una fuente secundaria de ondas que emite ondas secundarias (indicadas por los semicírculos pequeños), que llegan a la siguiente capa de partículas del medio. Estas partículas se ponen entonces en movimiento, formando la siguiente superficie de onda S', que es tangente a las ondas secundarias. El proceso se repite y produce la propagación de una onda en el medio.
Esta representación gráfica de la propagación parece muy razonable para una onda elástica que resulta de la vibración de átomos o moléculas de un cuerpo. Sin embargo, la construcción de Huygens no tiene significado físico en casos como, por ejemplo, una onda electromagnética que se propaga en el vacío, en el que no hay partículas en vibración. Por consiguiente, requirió una revi- sión cuando se admitió la existencia de otras ondas de tipo distinto. A fines del siglo XIX Kirchhoff sustituyó la construcción intuitiva de Huygens por un tratamiento más matemático y general. El movimiento ondulatorio está regulado por la ecuación de onda 28.11, que en tres dimensiones es
donde puede ser el desplazamiento de los átomos de una sustancia en el caso de una onda elástica, el campo eléctrico o el magnético en el caso de una onda electromagnética, etc. El análisis de la propagación de ondas en cualquier medio dado consiste en obtener una solución de la ecuación de onda que satisfaga las condiciones físicas del problema, esto es, la posición y naturaleza de las fuentes, las superficies físicas de discontinuidad, etc. A éstas se les conoce como condiciones de contorno. La teoría de ecuaciones diferenciales establece que, en condiciones especiales, podemos hallar una solución de una ecuación como la sin hacer referencia a las fuentes, si conocemos los valores de sobre una superficie S . Supongamos que deseamos evaluar el movi miento ondulatorio en un punto P. Si conocemos las fuentes O O O podemos sumar sus contribuciones en P para obtener el movimiento ondulatorio resultante. Pero si sólo conocemos los valores de en los puntos de la superficie cerrada arbitraria S que encierra a todas las fuentes, también podemos obtener la onda en P, aun si desconocemos la distribución de las fuentes. Entonces el principio de Huygens, modificado por Kirchhoff, es equivalente a decir que
podemos obtener la perturbación en un punto P en el tiempo t si conocemos la perturba- ción en cada elemento de superficie dS sobre una superficie S y suponemos que los elemen- tos de superficie actúan como fuentes de ondas secundarias. El movimiento ondulatorio en cualquier punto se obtiene sumando los movimientos ondulatorios debidos a estas fuentes secundarias.
Difracción de Fraunhofer producida por una ranura rectangular
En el caso de ondas que inciden perpendicularmente sobre una ranura rectangular muy estrecha larga, sólo la parte del frente de onda que pasa por la ranura contribuye a las ondas transmitidas difractadas. De acuerdo con el principio de Huygens, la distribución de intensidades de las ondas difractadas se obtiene sumando las ondas emitidas por cada punto situado entre A y E considerados como fuentes secundarias de ondas. Al observar las ondas difractadas a ángulos diferentes con respecto a la dirección de incidencia, encontramos que para ciertas direcciones su intensidad es cero.
Difracción de Fraunhofer producida por una abertura circular
Cuando en una pantalla que tiene una abertura circular inciden perpendicularmente ondas planas, el patrón de difracción consiste en un disco brillante rodeado por anillos oscuros y brillantes que se alternan, como se muestra en una de las figuras . El radio del disco central y de los anillos sucesivos no siguen una secuencia sencilla. Omitiremos el análisis matemático del problema, que es mucho más complicado que en el caso de una ranura rectangular.
Difracción de Fraunhofer producida por dos ranuras paralelas iguales
Consideremos dos ranuras, cada una de ancho b, desplazadas una distancia a . Para una dirección correspondiente al ángulo 0, tenemos dos conjuntos de ondas difractadas que llegan de cada ranura y el patrón que observamos es resultado de la interferencia de tales ondas difractadas. En otras palabras, tenemos ahora una combinación de difracción e interferencia.
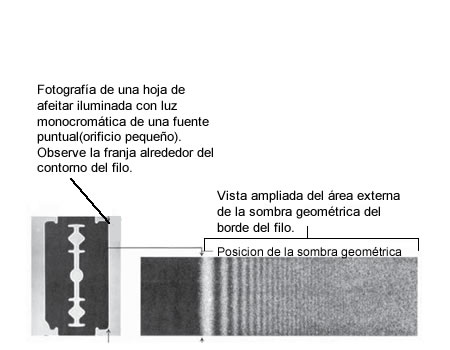 Patrón de difracción por un borde recto tal como el filo de una navaja.
Patrón de difracción por un borde recto tal como el filo de una navaja.Supongamos que un haz de luz monocromática incide sobre el filo de una hoja de afeitar . La mitad de la superficie de onda S es interrumpida por la navaja. Cada punto del frente de onda que está a la derecha de la navaja actúa como una fuente secundaria, según el principio de Huygens modificado por Kirchhoff. Por consiguiente, la luz que incide en una pantalla situada detrás de la navaja es resultado de la interferencia de las ondas secundarias producidas por la mitad de la onda original, dando como resultado la distribución de intensidades que se muestra en la figura . La intensidad disminuye gradualmente hasta cero dentro de la sombra geométrica y fluctúa durante las primeras longitudes de onda dentro de la región geométrica de iluminación. En los puntos que están directamente detrás del bor de, la intensidad es de un cuarto de la intensidad sin la pantalla. Esto se debe a que la pantalla detiene d paso de la mitad del frente de onda, dando como resultado una amplitud reducida a un medio y, en consecuencia, una intensidad reducida a un cuarto.
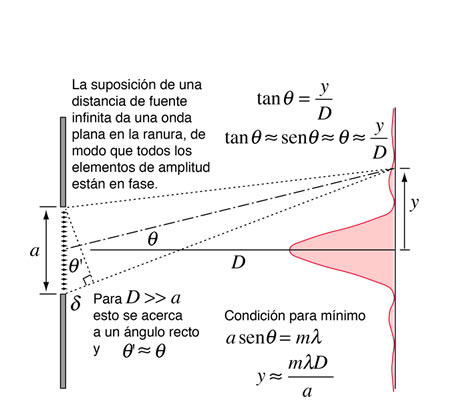 Geometría de la Difracción de Fraunhofer
Geometría de la Difracción de FraunhoferAunque el requisito formal de difracción de Fraunhofer es el de una distancia de pantalla infinita, por lo general se obtienen resultados de difracción razonables si la distancia de pantalla D >> a. Pero un requisito adicional es D>> a2/λ que surge del criterio de Rayleigh aplicado a una sola rendija. Si no se cumplen las condiciones para la difracción de Fraunhofer, es necesario utilizar el método de difracción de Fresnel.
 Difracción para Diferentes Anchos de Rendija Simple
Difracción para Diferentes Anchos de Rendija SimpleSe fotografiaron estos patrones de difracción de rendija simple con una fuente de luz de láser helio-neón y una rendija simple controlada por un micrómetro. Los bocetos de las anchuras de las rendijas de arriba a la derecha, se ampliaron por la distancia del primer mínimo de los patrones de difracción. Si la geometría es tal que se puede dar por válida la aproximación para ángulo pequeño, entonces los anchos de los patrones son inversamente proporcionales a las anchuras de las rendijas.
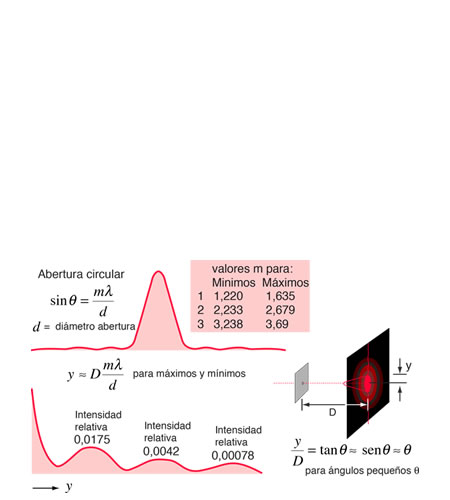 Difracción Abertura Circular
Difracción Abertura CircularCuando la luz de una fuente puntual pasa a través de una abertura circular pequeña no produce como imagen un punto brillante, sino más bien un disco difuso circular conocido como disco de Airy, rodeado de anillos circulares concéntricos mucho más tenues. Este ejemplo de la difracción es de gran importancia, porque tanto el ojo humano como muchos instrumentos ópticos, tienen aberturas circulares. Si esta deformación de la imagen de la fuente puntual, es mayor que la producida por las aberraciones del sistema, se dice que el proceso de imágenes está limitado por difracción, y que es lo mejor que se puede hacer con ese tamaño de abertura. Esta limitación en la resolución de las imágenes se cuantifica en términos del criterio de Rayleigh, de modo que se puede calcular el límite de resolución de un sistema.
